Ассиметрия букмекерства

В сегодняшнем материале мы обсудим варианты ассиметрии букмекерства. Расскажем о двух видах неопределенности и рассмотрим их модели в отношение ставок на спорт. Также окунемся в реальный мир заключения пари и выясним некоторые секреты букмекеров.

Многие участники игрового сообщества предполагают, что выиграть у букмекера практически невозможно или очень сложно. Однако они в большинстве своем не могут объяснить, в чем же именно заключается эта сложность. Предлагаем выяснить все преимущества конторы перед игроками и узнать, как на самом деле обстоят дела в этом плане.

Стоит сразу определить момент, когда игрок обыгрывает букмекера - это происходит во время перекрытия букмекерской маржи. Но в долгосрочной перспективе лишь немногим профессиональным бетторам удается это сделать. То есть, даже при минимальной марже в 2%, как у компании Pinnacle, обеспечить себе прибыль будет не самой простой задачей. Так что же мешает участникам игрового сообщества побеждать чаще и как конторе удается всегда оставаться в плюсе? - разберемся в нашем обзоре.

Много ли профессионалов среди игроков на ставках?

Начнем с того, что заключение пари абсолютно всегда напрямую связано с неопределенностью. С подобным эффектом сталкиваются абсолютно все игроки и пытаются понизить до максимума влияние этого воздействия для получения прибыли в долгосрочной перспективе. При поиске решения этой задачи можно прийти к пониманию того, насколько силен, на самом деле, букмекер и как сложно его одолеть при подобных условиях. Это и есть ассиметрия букмекерства, о которой поговорим более подробнее.

Существует два вида неопределенности. Случайная или статическая - это естественная неопределенность, которая основана на изменчивости самих вероятностей. Ее невозможно уменьшить и она является постоянной составляющей в ставках на спорт, с которой нужно смириться.

Второй тип - гносеологическая или модельная. Ее возникновение связано с непониманием модели прогнозирования или ситуации в целом. Дополнительные знания по такой модели помогают снизить уровень влияния подобной неопределенности и ее можно попытаться минимизировать.

В итоге получается, что главной целью игрока на ставках является уменьшение гносеологической неопределенности до уровня случайной. Однако на практике сделать это не так просто, как кажется - системы слишком сложные, да и характер реальности всегда вероятностный.

Моделирование неопределенности в ставках на спорт

В мире ставок для всех сторон процесса случайная неопределенность является постоянной и неизменной. Она равным образом действует и на игроков, и на букмекера, ведь реальность для всех одна. Смоделировать статистическую неопределенность довольно просто и здесь поможет генератор случайных чисел.

Для примера возьмем вероятность исхода события 50 на 50 (коэффициент 2.00). Используем генератор случайных чисел с выходным диапазоном значений от 0 до 1. При получении окончательного числа ниже 0.5 можно считать ставку выигрышной и наоборот. А само распределение выигрышных и проигрышных пари будет называться биномным.

Теперь попытаемся смоделировать гносеологическую неопределенность. Это будет сложнее сделать, не зная заранее распределение связанных с ней ошибок. Воспользуемся в данном случае распределением Гаусса. Для выборки возьмем 1 000 ставок с вероятностью выигрыша по каждой в 50%. За размер ошибки примем шесть стандартных отклонений - от 0 до 5% соответственно. На графике ниже продемонстрировано распределение «истинных» вероятностей выигрыша, где становится видно - чем шире распределение, тем выше гносеологическая неопределенность.

При инвертировании «истинных» вероятностей выигрыша можно получить распределение котировок, как показано на следующем графике:

Противостояние игрока и букмекера

Теперь можно использовать гносеологическую неопределенность в соревновании между игроком и букмекером. Для каждого события контора публикует предполагаемые котировки, уменьшая их на величину собственной маржи (2.5%). К примеру, если истинный коэффициент события составляет 2.00, то букмекер в линии укажет 1.95.

Что касается игрока, то здесь применяются иные методы оценки истинности котировок. При более «длинных» оценках от конторы, чем его собственные - игрок заключит пари на одну единицу. В ином случае он проигнорирует предложение. Размер выборки в этом случае - 10 000 ставок по методу Монте-Карло. График ниже показывает результаты для букмекера и игрока в этом соревновании.

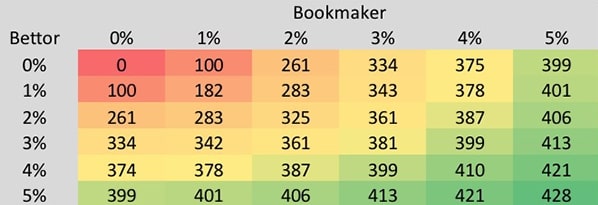
Становится очевидным, что при идеальных действиях обеих сторон ни одно пари не выиграет. Контора постоянно будет публиковать котировки 1.95, а игрок станет постоянно игнорировать подобные предложения, понимая, что они явно «короче» истинных. Следующая таблица демонстрирует ожидаемый выигрыш игрока для каждой пары неопределенностей. Стоит не забывать, что чем меньше отклонение, тем ниже гносеологическая неопределенность и лучше сама модель.

И теперь становится понятным, что при идеальных действиях букмекера игрок в любом случае будет терять деньги на уровне маржи в 2.5%, как бы он ни был хорош. Однако здесь кроется и шанс для успеха игрока - при плохой модели от конторы он всегда может рассчитывать на выигрыш, даже при более худшей собственной методике. Как же возникает подобный парадокс?

Для выяснения этого следует выяснить, как устроено само соревнование. Происходит это следующим образом: контора публикует котировки, игрок оценивает собственные шансы и принимает вызов при более «длинных» коэффициентах, а букмекер уже не может отменить свое предложение при этом.

Теперь предположим, что в этом случае присутствовала гносеологическая неопределенность. Значит, в 50% случаев ошибок конторы коэффициенты в действительности были «длиннее» фактических, а в 50% ошибок игрока - «короче». Подобная ассиметрия увеличивает соотношение между пари с отрицательным и положительным значением EV.

Чем выше гносеологическая неопределенность, тем выше будет и уровень ассиметрии. При условиях, описанных выше, в 56% случаев ставки будут иметь положительный баланс EV, а средние котировки составят 2.01. При увеличении стандартного отклонения до 5% количество выигранных ставок возростет до 68%, а среднее значение коэффициентов поднимется до 2.10.

Однако на практике добиться подобных результатов практически нереально. В теории предполагается, что модели игрока и букмекера не зависят друг от друга, а в жизни выходит так, что оба пользуются одними и теми же данными и похожими алгоритмами прогнозирования. Разница лишь в том, что у конторы есть немалый штат обученных аналитиков, а игрок действует в одиночку, что только снижает его шансы на успех.

Однако данная модель гносеологической неопределенности является ключевой при определении мастерства сторон. Игрок изначально считает, что котировки от букмекера считаются наиболее близкими к фактическим за вычетом маржи. Однако при неправильной оценки ситуации самой конторой она может оказаться в минусе, ведь отменить свое предложение, принятое игроком, уже не вправе.

В качестве вывода хотелось бы прояснить, что для победы над букмекером игроку необходимо иметь такое же мастерство прогнозирования и иметь на своей стороне ассиметрию. Это еще раз подтверждает предположение, что обыграть контору очень непросто, но возможно. Букмекеры, в отличие от игроков, не могут изначально знать, какая ставка считается хорошей и вполне могут ошибиться в своих оценках вероятностей. В этом и заключается шанс для участников игрового сообщества - следует внимательно искать подобные промахи и использовать их в свою пользу.