Что лучше делать для успешных пари: больше ставить или выбирать высокую ценность пари?

Стоит ли размещать ставки в больших количествах? Или ставки высокой ценности окажутся выгоднее? Читаем математический подход к теме ставок от авторов БК Pinnacle

Заинтересованные игроки на ставках часто обсуждают и следующий вопрос: выгоднее размещать большое количество ставок с низкой ценностью или несколько избранных ставок с высокой ценностью?

Что лучше для ставок: большое количество или высокая ценность?

Этот вопрос зачастую делит игроков на два лагеря. Те, кто считает, что ценность представляет собой самый важный аспект ставки, будут безустанно пытаться максимизировать ее. Они будут отказываться от возможностей с более низкой ценностью, так как прибыль по таким ставкам будет меньшей.

А вот представители другого лагеря будут настаивать на том, что важнее контролировать влияние дисперсии или удачи. Потому наиболее важно размещать большое количество ставок, пусть ценность каждой отдельно взятой ставки и будет ниже.

Под ценностью в мире размещения ставок понимается концепция, используемая для описания ожидаемого дохода на ставках. Математическое ожидание (или же EV) ставки показывает, сколько (предположительно) беттор выиграет или проиграет в среднем на каждой ставке.

Проще всего рассчитать это значение можно путем деления коэффициентов букмекера на истинные коэффициенты и вычитанием из результата единицы. Эта операция эквивалентна делению истинной вероятности исхода на предполагаемую букмекером вероятность с последующим вычитанием единицы.

Предположим, что истинные коэффициенты примерно равны 2. Если БК по ошибке предложит ставку с коэффициентами 2,1, то математическое ожидание будет составлять 2,1/2 – 1 = 0,05 (или 5 %). В результате размещения тысячи ставок по одной условной единице с одинаковым математическим ожиданием в среднем игрок получит прибыль размером 50 условных единиц.

А вот если букмекер предложит коэффициент 2,25, математическое ожидание возрастет до 12,5 %. Однако чаще всего ошибки совершают игроки. Если они примут коэффициенты величиной 1,95, математическое ожидание будет равно –2,5 %.

Средний результат является и наиболее вероятным. Однако везение (или невезение) также может повлиять на исходы пари в рамках одной серии. Ожидаемая прибыль от 1000 ставок с коэффициентами, равными двум, и с 5% ценностью может составлять 50 условных единиц. Но при удачном исходе мы получим больше, а при неудачном – меньше.

Ниже показано распределение возможных значений прибыли, которые мы можем получить в этом сценарии.

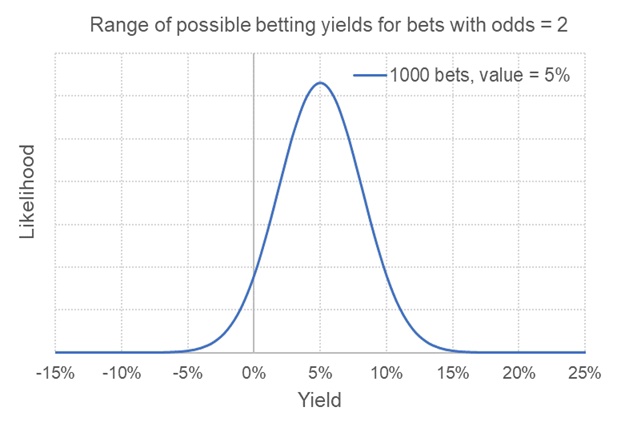
По распределению можно понять, что наиболее вероятный исход принесет 5% доходность. Если взять 1000 ставок по одной условной единице, то мы получим 50 условных единиц доходности. Кроме того, на наглядном примере можно увидеть диапазон вероятностей как для невероятно высокой удачливости, так и для катастрофического невезения. Вряд ли прибыль будет составлять менее –5 % или более +15 %.

Кроме того, визуально можно оценить вероятность проигрыша. Ему соответствует зона под кривой слева от вертикальной оси, где доходность равна 0%. Это значение также можно рассчитать математически. Оно составляет примерно 6%. Теперь можно увидеть, что произойдет с распределением возможных исходов, если изменится количество ставок. Ниже можно увидеть, как выполнены расчеты для 100 ставок, а также сравнены полученные распределения с первым.

Масштаб оси X увеличен, чтобы обе кривые были визуально различимы. Однако синяя кривая осталась неизменной. Гораздо важнее в данном случае возможность сравнить результаты.

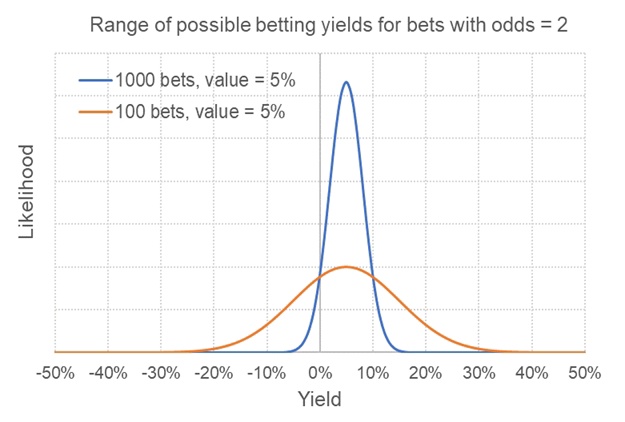
Тут в глаза бросаются два нюанса. Во-первых, мы имеем дело с гораздо более широким набором вероятностей. Тут чаще могут случаться крупные проигрыши и крупные выигрыши. Однако вероятность получения наиболее ожидаемого результата также немного понижается. Говоря терминами статистики, дисперсия увеличивается. Но на деле это просто еще один способ заявить о том, что в данном случае удача играет более важную роль.

Во-вторых, под кривой распределения теперь можно найти большую зону, которая относится к отрицательной доходности. Она составляет примерно 31%. Это означает, что пусть для этих 100 ставок ценность и равна 5%, существует вероятность проигрыша величиной почти в треть единицы. Увеличение количества ставок понизит дисперсию для возможных исходов и уменьшит влияние везения. Вероятность проигрыша для тех случаев, когда игрок обладает положительным математическим ожиданием.

Пока что счет равен 1:0 в пользу тех, кто предлагает размещать большее количество ставок.

Но это пока не конец. Люди, которые размещают ставки с большей избирательностью, делают это именно по причине того, что они гонятся за ставками с более высокой ценностью. Благодаря этому подходу их ожидаемая доходность будет выше. Для того чтобы отразить изменения, придется скорректировать оранжевую кривую. Среднее математическое ожидание для нашего игрока с одной сотней ставок с высокой ценностью равно 20 %. Насколько успешным окажется этот игрок по сравнению с первым игроком, которые размещает большое количество ставок?

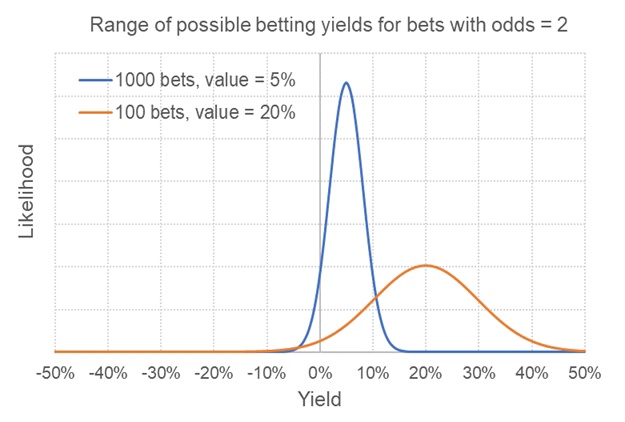
Распределение доходности для беттора с более ценными ставками все еще обладает той же формой. Однако оно смещено вправо на 15 процентных делений. Ожидаемая (средняя) доходность теперь равна 20%. Дисперсия исходов все еще настолько же высока. Однако теперь тут есть гораздо меньшее количество исходов без прибыли. Они составляют менее 2 % от общего количества. Это гораздо лучше, чем у первого игрока с 1000 ставок и математическим ожиданием, равным 5 %.

Можно удобно сравнить распределения этих двух игроков с помощью метрики, известной как «z-оценка». Для ее расчета ожидаемая доходность делится на стандартное отклонение распределения. Этот показатель – мера оценки ожидаемой доходности для единицы дисперсии. Чем значение этой метрики выше, тем лучше для игрока.

В финансовой сфере этот показатель обычно называют коэффициентом Шарпа. Стандартное отклонение, σ, является показателем вариации распределения. Квадрат этого показателя представляет собой простую дисперсию. Для серии ставок с одинаковыми коэффициентами o нашу метрику можно рассчитать с помощью следующего уравнения:

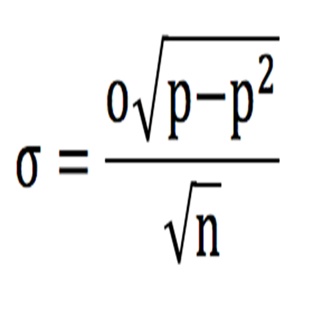
Тут p представляет собой истинную вероятность выигрыша ставки, а n – это количество ставок. Уравнение можно использовать и в тех ситуациях, когда приходится работать с различными коэффициентами, если размеры ставок остаются неизменными. В таком случае o просто соответствует усредненным коэффициентам.

Для расчета p просто нужно прибавить 1 к ожидаемой доходности, тогда получится ожидаемый доход. Его нужно разделить на коэффициенты. Наш игрок с большим количеством ставок и ожидаемой доходностью величиной 5 % (или 0,05) обладает p = (1 + 0,05)/2 = 0,525 или 52,5 %, и тогда σ = 0,0316 (или 3,16 %).

Примерно две трети всех возможных доходов в распределении игрока с большим количеством ставок находится в 3,16 % выше или ниже математического ожидания размером 5 %. Теперь можно рассчитать z-оценку: 5 % / 3,16 % = 1,58.

Выполнение аналогичных операций для игрока на ставках с высокой ценностью позволит получить z-оценку величиной 2,04. Это существенно превосходит результат игрока с большим количеством ставок.

Теперь счет в нашем соревновании между количеством и ценностью равен 1:1.

Увеличение количества снижает дисперсию исходов. Однако избирательность и достижение более высокой доходности может улучшить z-оценку и ожидаемую доходность на каждую единицу дисперсии.

До сих пор наугад были выбраны варианты математического ожидания и количества ставок. Математическое ожидание ставок игрока, предпочитающего высокую ценность, в четыре раза превосходило аналогичный показатель для игрока, выбирающего большое количество. При этом самих ставок было в десять раз меньше. Насколько реалистичны подобные цифры?

Крайне сложно найти ставки с математическим ожиданием 20 % и коэффициентами ставок, равными 2. Получится ли найти 100 таких ставок на каждую 1000 ставок с математическим ожиданием 5 %?  Непрямым методом оценки присутствующей на рынке ставок ценности может стать исследование движения цен.

Если предположить, что коэффициенты закрытия рынка (в среднем) представляют собой честный срез истинных коэффициентов, то величина предыдущих движений может использоваться для расчета приблизительной величины предшествующего математического ожидания. Оно могло существовать в коэффициентах.

Чем большее смещение произошло, тем большим является математическое ожидание. В среднем разница между двумя наборами коэффициентов является справедливым отражением истинного значения доступной ценности.

Использовав большой набор данных коэффициентов Pinnacle для футбольных матчей, соответствующих линиям открытия и закрытия, была рассчитана относительная доступность значений математического ожидания. Их в реальности можно найти на рынке. Результаты приведены ниже.

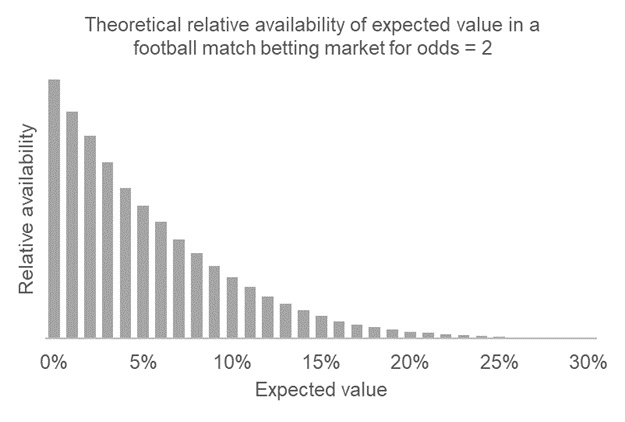
На этом рынке ставок было примерно в 20 раз больше доступных возможностей для размещения ставок с математическим ожиданием не ниже 5%, чем предложений с математическим ожиданием не ниже 20%. Если игрок, предпочитающий большое количество ставок, смог бы найти 1000 возможностей для размещения ставки с математическим ожиданием 5%, то беттору, выбирающему высокую ценность, удалось бы найти на том же рынке за то же время около 50 предложений. Это в два раза меньше моего изначального предположения.

Можно повторно рассчитать z-оценку для игрока, предпочитающего высокую ценность, с учетом этой информации о меньшем размере выборки. Теперь она равна 1,44. Это меньше аналогичного показателя игрока с большим количеством ставок. Вероятность проигрыша после этих 50 ставок теперь составляет 7,5 %.

Таким образом, с учетом относительной доступности различных значений математического ожидания игрок с более высоким оборотом в этом сценарии применяет более успешную стратегию с точки зрения управления рисками.

Количество увеличивает счет до 2:1 в поединке с ценностью.

Ранее учитывалась только доходность ставок. Но каждый игрок больше заинтересован в реальной прибыли. Доходность 5% от 1000 ставок предоставит прибыль величиной 50 единиц при размещении ставок по одной условной единице. А вот 20% доходность от 50 ставок принесет прибыль величиной 10 единиц.

Количество увеличивает отрыв от ценности до 3:1.

Конечно, любой защитник критерия Келли заявит, что ставки с более высоким математическим ожиданием должны приводить к большим размерам самих ставок. В этом случае, используя те же коэффициенты и в четыре раза большую ценность, можно обосновать увеличенный в четыре раза размер ставки. Он приведет к увеличению ожидаемой прибыли до 40 единиц, что гораздо ближе к 50 единицам прибыли первого игрока на ставках.

Ценность наносит ответный удар, выполнив несколько спорный пенальти.

Итоговый счет противостояния между количеством и ценностью равен 3:2. Количество побеждает с небольшим перевесом. Это упражнение помогает проиллюстрировать конкурентное преимущество снижения дисперсии (путем увеличения количества ставок) и увеличения математического ожидания (путем увеличения избирательности).

Как минимум на рынке размещения ставок на футбол не хватает возможностей размещения ставок с высоким математическим ожиданием, чтобы полностью оправдать выбор стратегии избирательного подхода к ставкам вместо того подхода, который подразумевает максимизацию количества и снижение дисперсии. Хотя разница между подходами оказалась не настолько существенной. Разные рынки могут предлагать различные пропорции возможностей, так что баланс подходов может сместиться в другую сторону.

Снижение дисперсии является отличной целью для любого игрока на ставках. Этот мысленный эксперимент должен продемонстрировать вам, что это не единственный фактор, который следует учитывать. Наиболее лучшее понимание относительного влияния количества и ценности ставок поможет любому амбициозному игроку максимизировать успехи при достижении цели.